Thông báo về workshop Thống kê Bayesian : 8h00 - 17h50 ngày 16 tháng 7 năm 2023
27/06/2023

Nhằm hướng đến mục tiêu tăng cường hợp tác quốc tế, giao lưu nghiên cứu khoa học với các trường cũng như góp phần nâng cao năng lực áp dụng các công cụ thống kê và kinh tế lượng trong nghiên cứu và giảng dạy và tăng cường vị thế của Trường Đại học Kinh tế TP.HCM trong lĩnh vực Toán và Thống kê ứng dụng, khoa Toán – Thống kê lập kế hoạch phối hợp với Viện Nghiên cứu cao cấp về Toán (VIASM), tổ chức Workshop về Thống kê Bayes.
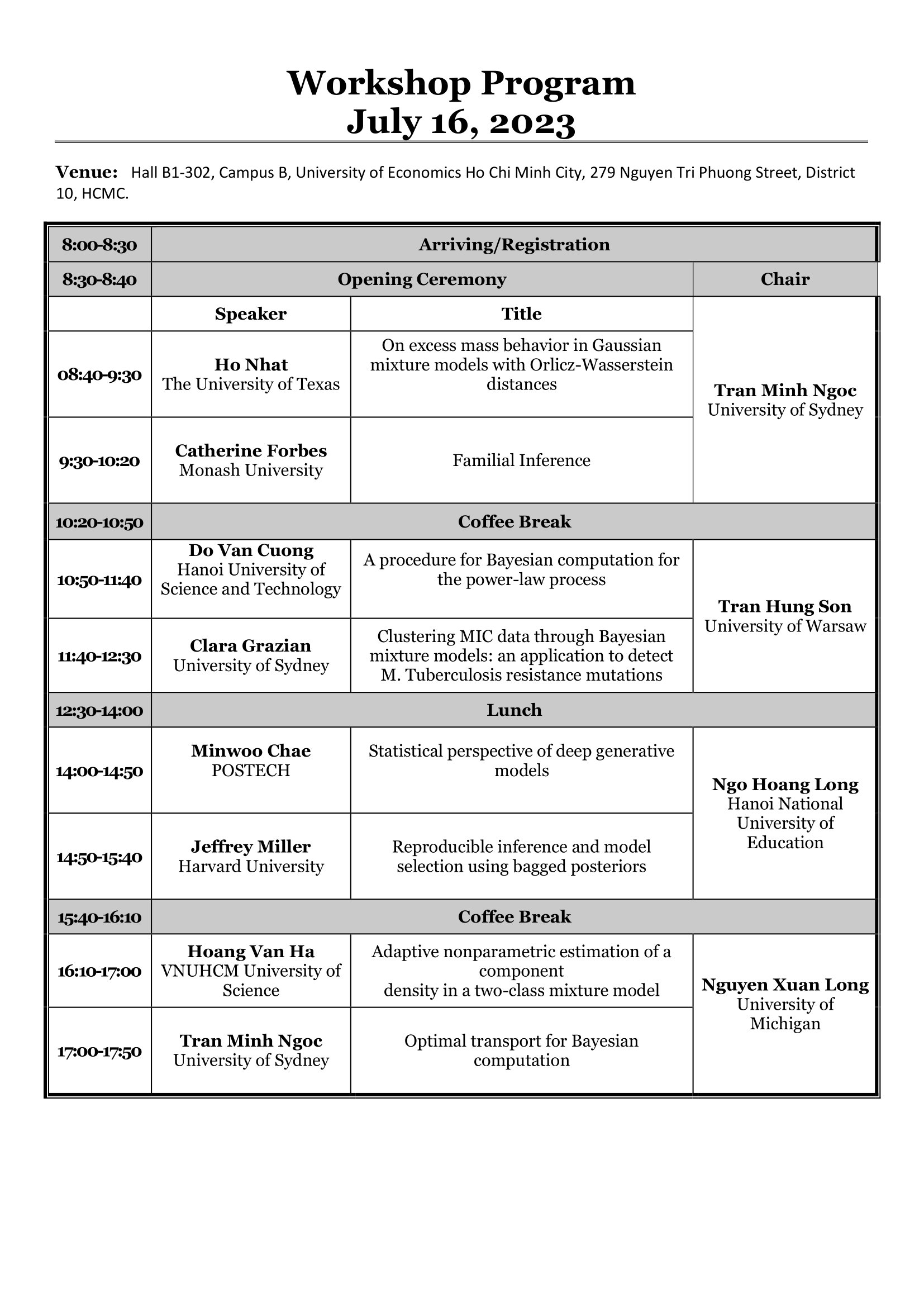
Thông tin cụ thể của workshop như sau:
Optimal Transport (OT) is a powerful mathematical theory that sits at the interface of several fundamental theories, including probability, optimisation, stochastic differential equations, and partial differential equations. It provides a mathematically elegant tool for solving optimisation problems on the space of probability measures. By equipping the space of probability measures with the Wasserstein distance, it can be made into a Riemannian manifold with a rich geometric structure, which is useful for both optimisation and sampling related statistical applications
In this talk, I will explore ways to use OT to design geometry-assisted and optimisation-guided Bayesian sampling techniques. Specifically, I will focus on the novel Particle Mean Field Variational Bayes (PMFVB) approach, which extends the classical MFVB method without requiring conjugate priors or analytical calculations. The theoretical basis of this new method is established by leveraging the connection between Wasserstein gradient flows and Langevin diffusion dynamics. I will demonstrate the effectiveness of the PMFVB approach using Bayesian logistic regression, stochastic volatility, and deep neural networks. Additionally, I will discuss the connection between the optimisation-based Particle Variational Bayes and sampling-based Sequential Monte Carlo, and how to improve the latter.
In the first part of this talk, we will provide a brief introduction to deep generative models, such as the variational autoencoder (VAE), generative adversarial networks (GAN), normalizing flows, and score-based methods, from a statistician's viewpoint. In the second part, we will focus on statistical theory for deep generative models, with an emphasis on VAE and GAN type estimators. Both VAE and GAN estimators achieve the minimax optimal rate in a classical nonparametric density estimation framework. Additionally, we will consider a structured distribution estimation where the target distribution is concentrated around a low-dimensional structure, allowing for singularity to the Lebesgue measure. The convergence rates of both estimators depend solely on the structure of the true distribution and the noise level. Moreover, GAN achieves a faster convergence rate than VAE. Finally, we will discuss the minimax optimal rate of the structured distribution estimation under consideration.
Dirichlet Process mixture models (DPMM) in combination with Gaussian kernels have been an important modeling tool for numerous data domains arising from biological, physical, and social sciences. However, this versatility in applications does not extend to strong theoretical guarantees for the underlying parameter estimates, for which only a logarithmic rate is achieved. In this work, we (re)introduce and investigate a metric, named Orlicz-Wasserstein distance, in the study of the Bayesian contraction behavior for the parameters. We show that despite the overall slow convergence guarantees for all the parameters, posterior contraction for parameters happens at almost polynomial rates in outlier regions of the parameter space. Our theoretical results provide new insight in understanding the convergence behavior of parameters arising from various settings of hierarchical Bayesian nonparametric models. In addition, we provide an algorithm to compute the metric by leveraging Sinkhorn divergences and validate our findings through a simulation study.
This talk is based on joint work with Aritra Guha and Long Nguyen.
Standard Bayesian inference is known to be sensitive to model misspecification, leading to unreliable uncertainty quantification and poor predictive performance. However, finding generally applicable and computationally feasible methods for robust Bayesian inference under misspecification has proven to be a difficult challenge. An intriguing approach is to use bagging on the Bayesian posterior ("BayesBag"); that is, averaging the posterior over many bootstrapped datasets. We provide theoretical results characterizing the asymptotic behavior of the BayesBag posterior under misspecification, and we empirically assess the BayesBag approach on synthetic and real-world data using a variety of models. Overall, our results demonstrate that BayesBag provides an easy-to-use and widely applicable approach that improves upon standard Bayesian inference by making it more stable, accurate, and reproducible.
Statistical hypotheses are translations of scientific hypotheses into statements about one or more distributions, often concerning their center. Tests that assess statistical hypotheses of center implicitly assume a specific center, e.g., the mean or median. Yet, scientific hypotheses do not always specify a particular center. This ambiguity leaves the possibility for a gap between scientific theory and statistical practice that can lead to rejection of a true null. In the face of replicability crises in many scientific disciplines, "significant results" of this kind are concerning. Rather than testing a single center, this paper proposes testing a family of plausible centers, such as that induced by the Huber loss function (the "Huber family"). Each center in the family generates a testing problem, and the resulting family of hypotheses constitutes a familial hypothesis. A Bayesian nonparametric procedure is devised to test familial hypotheses, enabled by a pathwise optimization routine to fit the Huber family. The favorable properties of the new test are verified through numerical simulation in one- and two-sample settings. Two experiments from psychology serve as real-world case studies.
Antimicrobial resistance is becoming a major threat to public health throughout the world. Researchers are attempting to contrast it by developing both new antibiotics and patient-specific treatments. In the second case, whole-genome sequencing has had a huge impact in two ways: first, it is becoming cheaper and faster to perform whole-genome sequencing, and this makes it competitive with respect to standard phenotypic tests; second, it is possible to statistically associate the phenotypic patterns of resistance to specific mutations in the genome. Therefore, it is now possible to develop catalogues of genomic variants associated with resistance to specific antibiotics, in order to improve prediction of resistance and suggest treatments. It is essential to have robust methods for identifying mutations associated to resistance and continuously updating the available catalogues. This work proposes a general method to study minimal inhibitory concentration (MIC) distributions and to identify clusters of strains showing different levels of resistance to antimicrobials. Once the clusters are identified and strains allocated to each of them, it is possible to perform regression method to identify with high statistical power the mutations associated with resistance.
The Power-Law Process (PLP) is a Poisson process with intensity function having a power form. It is frequently used to model repairable systems.
In this talk we propose a procedure for Bayesian computation for the Power-Law Pro-cess (PLP). The procedure consider noninformative prior then semiconjugate prior and full conjugate prior for the Bayesian analysis of the PLP. Metropolis-Hastings and Gibbs sam-pling algorithms are used for Bayesian computation when we consider an arbitrary prior distribution.
The proposed procedure is investigated with simulation study and a real data set in comparison to maximum likelihood estimation.
A two-class mixture model, where the density of one of the components is known, is considered. We address the issue of the nonparametric adaptive estimation of the unknown probability density of the second component. We propose a randomly weighted kernel estimator with a fully data-driven bandwidth selection method, in the spirit of the Goldenshluger and Lepski method. An oracletype inequality for the pointwise quadratic risk is derived as well as convergence rates over Hölder smoothness classes. The theoretical results are illustrated by numerical simulations. (Joint work with Gaëlle Chagny, Antoine Channarond (University of Rouen - Normandie) and Angelina Roche (Paris Dauphine University)).